Investigation of Copper(II) amino acid complexes
A metabolism for copper ions is widespread among living systems.
To help in the understanding of the binding of the ion in
biopolymers and physiological fluids, the prototype compounds of
cupric ions with amino acids have been extensively studied.
Bis (glycinato)copper(II).hydrate was first isolated in 1841 and
in 1890 a second form was discovered. It was later suggested that
the two modifications; one pale blue needles and the other bluish
violet glistening plates were geometric (cis/trans) isomers.
These compounds represent some of the first geometric isomers
discovered and recently the novel solid state thermal
isomerisation of the cis- to the trans- form was reported.
In this experiment, the formation of the copper(II) glycine
complexes will be studied as a function of pH and from the
titration data the overall stability constant b2 will be
calculated. In addition, IR spectroscopy will be used in
conjunction with a simple group theory approach to distinguish
between the cis- and trans- isomers of Cu(gly)2.H2O.
Part A-Stability Constant Calculations
The formation of metal complexes is often highly dependent on the
pH of the solution. This is because there is a competition for
the ligand between the metal ion and the proton as they both bind
to the same atoms of the ligand. For glycine at low pH, the metal
ion has to displace a proton from the amine N in order to form a
stable complex.
Cu2+(aq) + 2H3N+CH2COO- ⇔ Cu(NH2CH2COO)2 + 2H+(aq)
The number of protons displaced through chelate formation can
be determined from a pH titration of a mixture of ligand and
metal ion; in this instance a 2:1 mixture of glycine and Cu2+(aq)
is used. It is also necessary to do a pH titration of glycine
alone, so that the dissociation constants of the ligand can be
obtained.
For the ligand:
H3N+CH2COOH ⇔ H3N+CH2COO- (gly-) + H+(aq) Ka1
H3N+CH2COO- ⇔ H2NCH2COO- + H+(aq) Ka2
The stepwise stability constants K1 and K2 for the reaction of
the ligand with Cu2+ are given by the expressions:
Cu2+ + gly- ⇔ Cu(gly)+ K1 (β1)
Cu(gly)+ + gly- ⇔ Cu(gly)2 K2
and the overall stability constant β2 = K1 * K2
From the titration curve for glycine, the pH at 0.5 the
equivalence point gives pKa1 while at 1.5 gives pKa2.
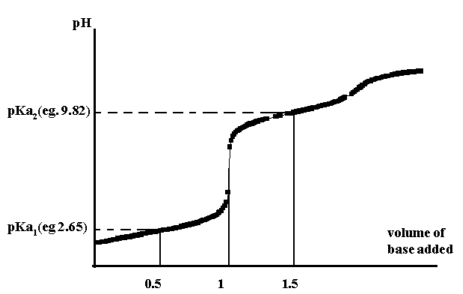
Figure 1.
To calculate the stability constants (K1 and K2) use is made
of the formation function, n, which is defined as the ratio of
total ligand bound to the total metal present:
n = { [Cu(gly)+] + 2[Cu(gly)2] } / { [Cu2+] + [Cu(gly)+] + [Cu(gly)2] }
substituting from equations (1) and (2) gives
n = { β1(gly-) + 2β2 [gly-]2 } / {1 + β1(gly-) + β2 [gly-]2}
From an experimental standpoint, this needs to be expressed in
terms of total copper(II) ions, total glycine and pH for the
calculation to be able to be carried out. When this is done, the
expression becomes:
[Hgly] = [Hgly]total - [H+] - [Na+] + [OH-] / (1+[H+]/Ka1)
and n = {[Hgly]total - [Hgly]}.{1+Ka2/[H+]+[H+]/Ka1} /[Cu2+]total
also [gly-] = Ka2.[Hgly]/[H+]
if n versus p(gly-) is plotted, then an approximate value of the
stepwise formation constants, K1 and K2, are obtained at =0.5 and
=1.5. A more accurate measure of β2 is obtained at =1.0.
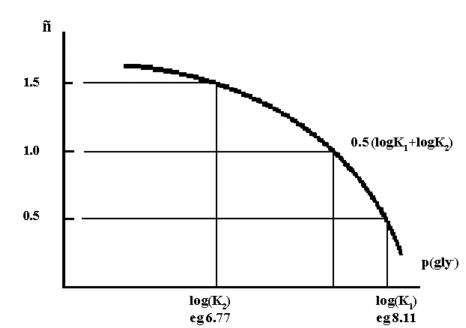
Figure 2.
A more precise method uses a simple linear least squares
analysis of the titration results and makes use of the equation:
n = {β1[gly-] + 2 β2 [gly-]2} / { 1+ β1[gly-] + β2[gly-]2 }
Rearrangement of which gives:
n/((1-n)[gly-]) = β1 + β2 * (2-n) * [gly-]/(1-n)
Thus a plot of n/((1-n)[gly-]) versus (2-n)[gly-]/(1-n)
should yield a straight line. Most programmable calculators can
do a least squares fit, else it can be done easily with a
spreadsheet application such as Excel.
To download a zipfile containing an Excel worksheet with a
template setup, use the link here.
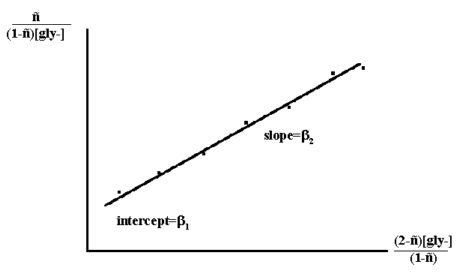
Figure 3.
Procedure.
Prepare the following stock solutions:
a) 500 cm3 of 0.1M NaOH. This should be standardised with potassium
hydrogen phthalate.
b) 500 cm3 of 0.1M HNO3. This should be standardised with the 0.1M NaOH
above.
c) 10 cm3 of 0.1M Cu(NO3)2 solution from 0.25g Cu(NO3)2.2.5H2O.
d) 250 cm3 of 0.05M KNO3.
Titration of Glycine
Weigh (to the nearest 0.1mg) a 0.1g sample of glycine into a 250
cm3 beaker. Pipette 100 cm3 of 0.05 KNO3 into the beaker, mix and
record the pH. Pipette 10 cm3 of standardised 0.1M HNO3 into the
beaker and record the new pH of the solution. Titrate the
solution with the standardised 0.1M NaOH, making sure to stir
continuously after each addition and to plot the titration curve
AS YOU PROCEED. Continue the titration until the number of moles
of base added is equal to the number of moles of HNO3 plus the
number of moles of glycine present.
Titration of the Copper-Glycine system
Weigh (to the nearest 0.1mg) a 0.1g sample of glycine into a 250
cm3 beaker. Pipette 100 cm3 of 0.05 KNO3 into the beaker, mix and
record the pH. Add by pipette, 2 cm3 of 0.1M copper(II) solution
and record the pH again. Titrate, using ~ 0.2 cm3 increments of
standard 0.1M NaOH, with continuous stirring. Note: the
calculations give the best results when the first five or six
data points from the titration curve are used.
Preparations.
cis-Cu(gly)2.H2O
Copper(II) acetate monohydrate (0.01 mole, 2.0 g) is dissolved in
25 cm3 of hot water. 25 cm3 of hot ethanol is added and the
solution kept hot. Glycine(0.02 mole, 1.5 g) is dissolved in 25
cm3 of hot water. The solutions are mixed while hot (~70C) and
the solution then cooled on ice. A needle-like precipitate is
obtained. Record the yield. Preserve the filtrate.
trans-Cu(gly)2.H2O
Two methods have been used for the preparation of the trans-
isomer, but the first gives the cleaner product.
a) 10 cm3 of the filtrate above is placed in a small flask with
~ 1.5 g of the cis- isomer and 1 g of glycine. The suspension is
heated under reflux for one hour. The hot mixture is then
filtered to give the trans-Cu(gly)2.H2O. Note that if the mixture
all dissolves during the reflux, then the cis-product will
reprecipitate not the trans-.
b) An alternative method, is to place a small quantity of the
cis-isomer in an oven at 170¦C for an hour. On cooling in
air, this leads to the solid state conversion to the
trans-isomer.
Part B IR spectra of cis- and trans- Cu(gly)2. H2O
It should be possible to distinguish between the two isomers by
considering the immediate environment around the central metal
and assuming that their vibrations are independent of the motions
involving the rest of the atoms of the ligands.
IR spectra (KBr pellet 4400-400 cm-1) in JCAMP-DX format
cis-isomer
trans-isomer
That is, by considering only the Cu and the N and O atoms, the
cis-isomer will have C2v symmetry, whilst the trans-isomer D2h
symmetry.
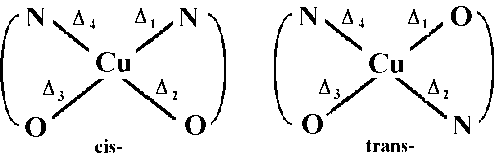
Figure 4.
The reducible representations for C2v and D2h are:
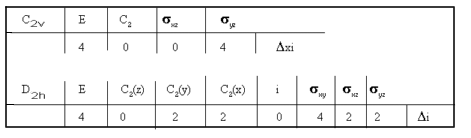
Figure 5.
and using the reduction formula, then for:
C2v → 2A1 + 2B2 all bands should be IR active,
while for
D2h → 2A1g + B2u + B3u only the B2u and B3u bands
should be IR active, the 2A1g symmetric bands being Raman active.
It is expected therefore that for the metal-ligand stretching
vibrations, 4 bands should be observed in the IR spectrum of the
cis-isomer, but only 2 bands for the trans-isomer. Since N is the
lighter atom it is also expected that the M-N modes will be at
higher energy than the M-O modes.
Interpretation.
The metal-ligand stretching modes occur below 500 cm-1. From the
spectra in the Appendix tabulate all peaks in that region. (Note:
the band at ~380 cm-1 is common to both spectra and has been
described as a skeletal band and will not be used in the
interpretation).
For the cis-isomer, assign v asymmetric and v symmetric bands
for M-N and M-O. For the trans-isomer, assign v asymmetric for
M-N and M-O.
From the spectra recorded on your samples (4000-600 cm-1),
tabulate the major peaks and assign as many bands as possible.
Can you make use of another region in these spectra to
distinguish between the two isomers?
Questions.
1) The use of Cu(II) salts, including those of simple
amino-acids, has been described for the treatment of rheumatoid
arthritis. How is the copper thought to act? Give two references
outlining this work.
2) A number of copper containing enzymes are known. Give the
names of two of these and show the coordination environment
around the copper.
3) It has been claimed that to a good approximation
log K1 = pKa2-pH-log([L] - 1/2 [Cu])
where [L]=total ligand concentration in all forms and
[Cu]=total copper concentration in all forms
pKa1 is the value for glycine and pH is the pH of the copper
glycine mixture when one quarter of the glycine has been
titrated.
Also that
log K2 = pKa2-pH-log([L] - 3/4 [Cu])
where the pH is now taken when three quarters of the glycine is
titrated.
Use your titration results to show whether this approximation
gives reasonable results.
References
J.J. Farrell, J. Chem. Educ., 54, 1977, 445.
P. O'Brien, J. Chem. Educ., 59, 1982, 1052.
return to list of C31L
experiments
Copyright © 2005 by Robert John Lancashire, all rights
reserved.
Created and maintained by Prof. Robert J.
Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.
Created November 1995. Links checked and/or last
modified 10th November 2005.
URL
http://wwwchem.uwimona.edu.jm/lab_manuals/c31lex1.html
 Figure 1.
Figure 1.
 Figure 1.
Figure 1.
 Figure 2.
Figure 2. Figure 3.
Figure 3.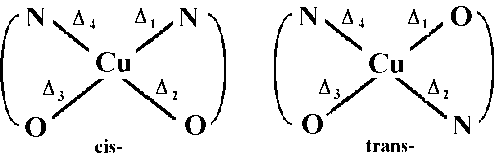 Figure 4.
Figure 4. Figure 5.
Figure 5.