
These complexes contain a central atom or ion, often a transition metal, and a cluster of ions or neutral molecules surrounding it. Many complexes are relatively unreactive species remaining unchanged throughout a sequence of chemical or physical operations and can often be isolated as stable solids or liquid compounds.
Other complexes have a much more transient existence and may exist only in solution or be highly reactive and easily converted to other species.
All metals form complexes, although the extent of formation and nature of these depend very largely on the electronic structure of the metal.
The concept of a metal complex originated in the work of Alfred Werner, who in 1913 was awarded the first Nobel Prize in Inorganic chemistry. A description of his life and the influence his work played in the development of coordination chemistry is given by G.B. Kauffman in "Inorganic Coordination Compounds", Heyden & Son Ltd, 1981.
Complexes may be non-ionic (neutral) or cationic or anionic, depending on the charges carried by the central metal ion and the coordinated groups. The total number of points of attachment to the central element is termed the coordination number and this can vary from 2 to greater than 12, but is usually 6.
The term ligand (ligare [Latin], to bind) was first used by Alfred Stock in 1916 in relation to silicon chemistry. The first use of the term in a British journal was by H. Irving and R.J.P. Williams in Nature, 1948, 162, 746 in their paper describing what is now called the Irving-Williams series.
For a fascinating review of the origin and dissemination of the term 'ligand' in chemistry see: W.H. Brock, K.A Jensen, C.K. Jorgensen and G.B. Kauffman, Polyhedron, 2, 1983, 1-7.
Ligands can be further characterised as monodentate, bidentate, tridentate etc. where the concept of teeth (dent) is introduced, hence the idea of bite angle etc.
The term chelate was first applied in 1920 by
Sir Gilbert T. Morgan and H.D.K. Drew [J. Chem. Soc.,
1920, 117, 1456], who stated:
"The adjective chelate, derived from the great claw or
chela (from the Greek χηλη) of the lobster or other
crustaceans, is suggested for the caliperlike groups which
function as two associating units and fasten to the central atom
so as to produce heterocyclic rings."

Metal complexation is of widespread interest. It is studied not only by inorganic chemists, but by physical and organic chemists and by biochemists, pharmacologists, molecular biologists and environmentalists.
Consider the four steps involved in the formation of the cuprammonium ion Cu(NH3)42+:
STEP 1: Cu2++NH3 ⇄ Cu(NH3)2+The addition of the four ammine groups to copper shows a pattern found for most formation constants, in that the successive stability constants decrease. In this case, the four constants are:
logK1 =4.0, logK2 =3.2, logK3 =2.7, logK4 =2.0 or logβ4 =11.9It is usual to represent the metal-binding process by a series
of stepwise equilibria. This can lead to stability constants that may
vary numerically from hundreds to enormous values such as
1035 and more.
That is
100,000,000,000,000,000,000,000,000,000,000,000.0
For this reason, they are commonly reported as logarithms.
so log10 (β) = log10 (1035) = 35.
For this reason it is useful to use logarithms, since log(K) is
directly proportional to the free energy of the reaction.
It has been known for many years that a comparison of this type always shows that the complex resulting from coordination with the chelating ligand is much more thermodynamically stable. This can be seen by looking at the values for adding two monodentates compared with adding one bidentate, or adding four monodentates compared to two bidentates, or adding six monodentates compared to three bidentates.
| # of ligands | ΔG⦵ /kJmol-1 | ΔH⦵ /kJmol-1 | ΔS⦵ /JK-1mol-1 | log β |
| 2 NH3(1 en) | -28.24 (-33.30) | -29.79 (-29.41) | -5.19 (+13.05) | 4.95 (5.84) |
| 4 NH3(2 en) | -42.51 (-60.67) | -53.14 (-56.48) | -35.50 (+13.75) | 7.44 (10.62) |
| # of ligands | log β | ΔG⦵ /kJmol-1 |
| 2 py (1 bipy) | 3.5 (6.9) | -20 (-39) |
| 4 py (2 bipy) | 5.6 (13.6) | -32 (-78) |
| 6 py (3 bipy) | 9.8 (19.3) | -56 (-110) |
| # of ligands | log β | ΔG⦵ /kJmol-1 |
| 1 NH3 | 2.8 | -16 |
| 2 NH3 (1 en) | 5.0 (7.51) | -28.5 (-42.8) |
| 3 NH3 | 6.6 | -37.7 |
| 4 NH3 (2 en) | 7.87 (13.86) | -44.9 (-79.1) |
| 5 NH3 | 8.6 | -49.1 |
| 6 NH3 (3 en) | 8.61 (18.28) | -49.2 (-104.4) |
In the case of complex formation of Ni2+ with ammonia or 1,2-diaminoethane, by rewriting the equilibria, the following equations are produced.
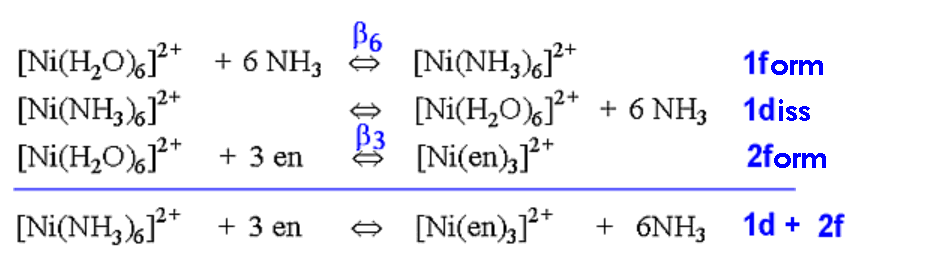
ΔG⦵ = -2.303 RT log10 (K)Based on measurements made over a range of temperatures, it is possible to break the ΔG⦵ term down into its enthalpy and entropy components. ΔG⦵ = ΔH⦵ - TΔS⦵
= -2.303 R T (18.28 - 8.61)
= -54 kJ mol-1
ΔH⦵ = -29 kJ mol-1
- TΔS⦵ = -25 kJ mol-1
and at 25 °C (298 K)
ΔS⦵ = +88 J K-1 mol-1
ΔG⦵ = -67 kJ mol-1The conclusion they drew from these incorrect numbers was that the chelate effect was essentially an entropy effect, since the TΔS⦵ contribution was nearly 5 times bigger than that of ΔH⦵.
ΔH⦵ = -12 kJ mol-1
- TΔS⦵ = -55 kJ mol-1
In fact, the breakdown of the ΔG⦵ into ΔH⦵
and TΔS⦵ shows that the two terms are nearly equal (-29
cf. -25 kJ mol-1) with the ΔH⦵ term a little
larger! The entropy term found is still much larger than for ordinary
reactions involving substitution of a non-chelating ligand at a metal ion.
How can we explain this enhanced contribution from entropy? One
explanation is to count the number of species on the left and
right hand side of the equation above.
It will be seen that on the left-hand-side there are 4 species,
whereas on the right-hand-side there are 7 species, that is a net
gain of 3 species occurs as the reaction proceeds. This can
account for the increase in entropy since it represents an
increase in the disorder of the system.
An alternative view comes from trying to understand how the
reactions might proceed. To form a complex with 6 monodentates
requires 6 separate favourable collisions between the metal ion
and the ligand molecules. To form the tris-bidentate metal
complex requires an initial collision for the first ligand to
attach by one arm but remember that the other arm is always going
to be nearby and only requires a shift in position of the other end to
enable the ligand to form the chelate ring.
If you consider dissociation steps, then when a monodentate group
is displaced, it is lost into the bulk of the solution. On the
other hand, if one end of a bidentate group is displaced the
other arm is still attached and it is only a matter of the arm
shifting around and it can be reattached again.
Both sets of conditions favour the formation of the complex with
bidentate groups over that with monodentate groups.
For a problem relating to metal complex formation and calculations of thermodynamic values, try your hand at CALCULATION # TWO. Once again, further problems can be found in the Tutorial papers for this course.
To get a simplistic view of the replacement of ammonia groups
by 1,2-diaminoethane try downloading a movie clip (1.7 MB, .avi format).
Note, for those linking from off-campus this may not
be possible due to bandwidth and timeout problems!
 Return to Chemistry, UWI-Mona,
Home Page
Return to Chemistry, UWI-Mona,
Home Page
Copyright © 1995-2015 by Robert John Lancashire, all rights reserved.
Created and maintained by Prof. Robert J. Lancashire,