In the ionic CFT, it is assumed that the ions are simple point charges. When applied to alkali metal ions containing a symmetric sphere of charge, calculations of bond energies are generally quite successful. The approach taken uses classical potential energy equations that take into account the attractive and repulsive interactions between charged particles (that is, Coulomb's Law interactions).
The bond energy between the charges is proportional to q1 * q2/r
where q1 and q2 are the charges of the interacting ions and r is the distance separating them. This leads to the correct prediction that large cations of low charge, such as K+ and Na+, should form few coordination compounds.For transition metal cations that contain varying numbers of d electrons in orbitals that are NOT spherically symmetric, however, the situation is quite different. The shape and occupation of these d-orbitals then becomes important in an accurate description of the bond energy and properties of the transition metal compound.
To be able to understand and use CFT then, it is essential to have a clear picture of the shapes (angular dependence functions) of the d-orbitals.
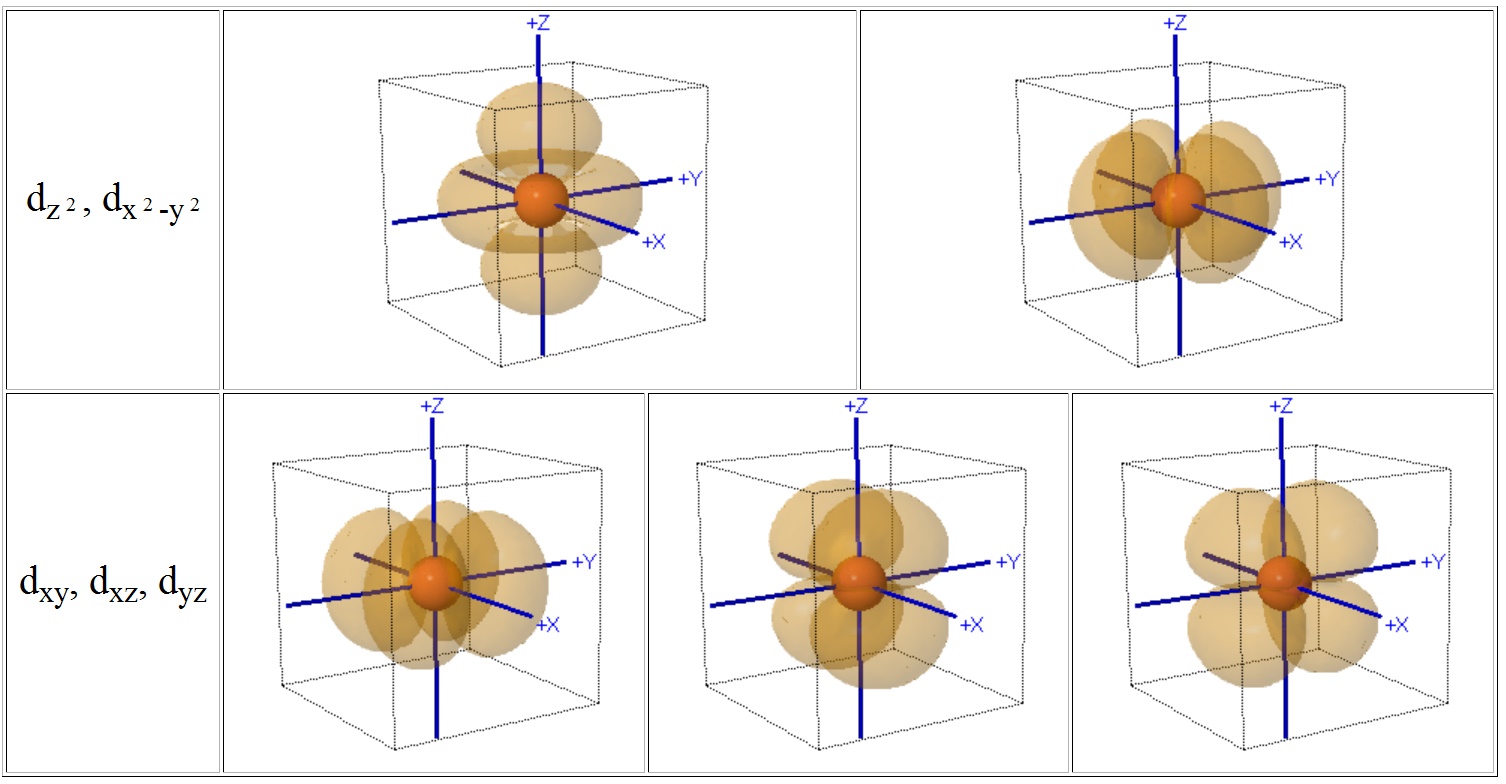
A cube provides a convenient reference for displaying the coordination centre of complexes since octahedral compounds have cubic symmetry i.e. the six anions sit at the centres of the faces of the cube and for tetrahedral complexes the 4 ligands sit at opposite diagonal edges.
You should be able to see that two of the d-orbitals, the dz2 and dx2-y2 meet the faces of the cube, but the remaining three (dxy, dyz and dxz) point towards the edges of the cube and actually have a node meeting the centres of the faces.
What happens then to the energy of the d-electrons if negatively charged ligands are brought in towards the metal centre to give an octahedral complex - where the ligands sit at the centre of the faces of the cube i.e. on the X, Y and Z axes? Since the d electrons are themselves negatively charged they would experience repulsion and their energies would be raised. For 's' and 'p' electrons this is of little consequence but for 'd' electrons there will be an energy difference involved depending on the orbital distribution and occupation.
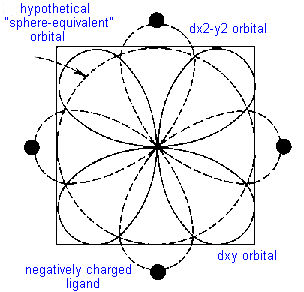
Consider the simple example of TiCl63- in which six chloride ions octahedrally surround the Ti3+ cation. There is only one d-electron to be allocated to one of the five d- orbitals. If it were to occupy the dz2 or dx2-y2 orbital, both of which meet the face of the cube and thus point directly towards the chloride ligands, it would be strongly repelled. The geometry of these orbitals and their nodes would require the electron to stay near the negatively charged ligands causing even more repulsion than a spherically distributed electron would experience. On the other hand, if the electron were to occupy the dxy, dyz or dxz orbital, it would spend less time near the ligands than would a spherically distributed electron and would be repelled less.
This difference between for example the dx2-y2 orbital, the dxy orbital and a spherical distribution can be graphically represented by
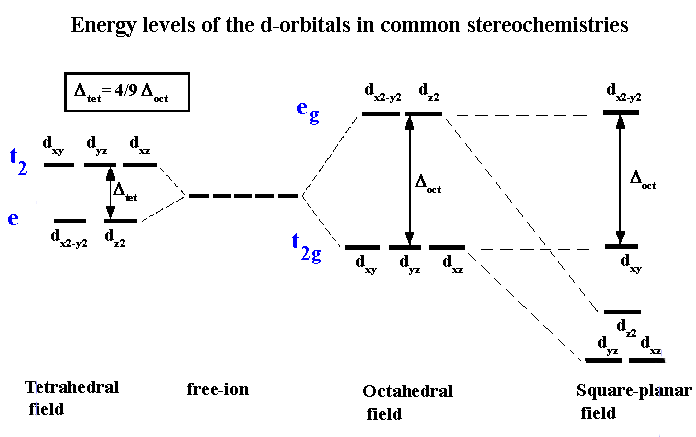
The next step is to consider how the d-orbitals interact with these incoming ligands. For tetrahedral complexes, the energy of those orbitals which point towards the edges should now be raised higher than those which point towards the faces. That is, the exact opposite of the situation we just dealt with for the octahedral crystal field. The end result is a splitting pattern which is represented in the splitting diagram above.
The square planar case can be considered as an extension of the octahedral, where we remove the two ligands from the Z axis. Consequently, repulsion of an electron in the dz2 orbital will no longer be equivalent to that experienced by an electron in the dx2-y2 orbital, and the end result is shown above. For the first year course, the only square planar complexes will be for d8 complexes, i.e all four coordinate complexes are tetrahedral except for d8 which may be tetrahedral or square planar.
Once we accept that the energy of the 5 'd' orbitals are no longer degenerate in a coordination compound we can begin to explore some of the implications. Note that a different CFT energy splitting diagram has to be applied for each stereochemistry. In this course we will only be concerned with diagrams for octahedral, tetrahedral and square planar complexes.
One of the important aspects of CFT is that not all ligands are identical when it comes to causing a separation of the energy of the d-orbitals. For transition metal compounds, there is clear evidence for this from the multitude of colours available for a given metal ion when the ligands or stereochemistry are varied. For octahedral complexes this is a reflection of the energy difference between the higher dz2, dx2-y2 (eg subset) and the dxy, dyz, dxz (t2g subset).
It has been established that the ability of ligands to cause a large splitting of the energy between the orbitals is essentially independent of the metal ion and the SPECTROCHEMICAL SERIES is a list of ligands ranked in order of their ability to cause large orbital separations.
A shortened list includes: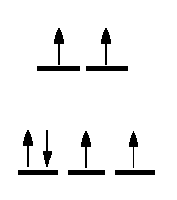
A simple JAVA applet that shows the electronic configuration for octahedral and tetrahedral complexes and calculates the spin-only magnetic moment is available.
One method of determining the number of unpaired electrons is by looking at the magnetic properties of the compounds. A simple technique to determine a magnetic moment (the GOUY METHOD) involves weighing the sample in the presence and absence of a strong magnetic field. By careful calibration using a known standard, such as Hg[Co(SCN)4] the number of unpaired electrons can be determined.
To predict the magnetic moment, we can use the simple
spin-only formula:
μ = √[4S(S+l)] Bohr Magneton (BM)
where S is the spin quantum number (1/2 for each unpaired
electron).
μ = √[n(n+2)] Bohr Magneton (BM)
where n is the number of unpaired electrons.
It is expected that all students will be able to calculate the spin-only magnetic moment of any coordination compound. To do this, you must know the number of d-electrons in the central metal ion, the stereochemistry and whether weak field-strong field considerations are necessary.
| K3[Fe(oxalate)3] 3H2O | K2[CuCl4] | |
| metal ion | Fe3+ | Cu2+ |
| number of d electrons | 5 - t2g3 eg2 | 9 - e4 t25 |
| stereochemistry | octahedral | tetrahedral |
| High Spin/Low Spin | High Spin | Not relevant (all High spin) |
| # of unpaired electrons | 5 | 1 |
| magnetic moment | √(35) B.M | √(3) B.M |
Other examples can be found in the Tutorial paper for this course.
 Return to Chemistry, UWI-Mona,
Home Page
Return to Chemistry, UWI-Mona,
Home Page
Copyright © 1996-2015 by Robert John Lancashire, all rights reserved.
Created and maintained by Prof. Robert J. Lancashire,