Appendix 7: Analysis of error in the slope and the
intercept of a linear plot using the 'Box" method.
The 'Box' method is a fast and simple way of determining the
uncertainty or error in the slope and intercept of a linear plot.
When a plot is made of several points, under experimental
conditions in the laboratory, usually there is some amount of
scattering. The scattering is usually about some best straight
line, drawn so that there is equal (as best as possible) scatter
on both sides of it.
NB.The best straight line does not have to
touch, or pass through, any of the plotted points.
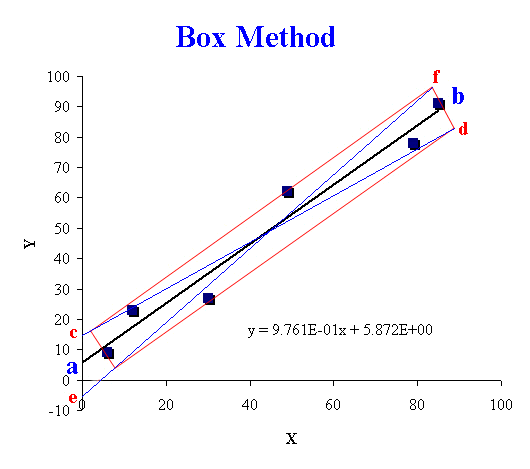
For the above plot, which has six (6) points, the best
straight line is shown by the line ab.
After the best straight line is drawn, the 'box', which is a
rectangle, is drawn so as to just enclose all 6 points. There can
only be 1 box that uniquely describes the data and this is chosen
using the point lowest from the line and highest above the line
and the point to the far left and furthest right as shown.
At this point it would be good to note that if one or two points
seem to be very far off the best straight line then it may be possible
to 'exclude' them. Tests on significance can be run to determine
whether these points, called 'outliers', can be legitamately ignored.
The next step is to find the gradient of the lines forming the
diagonals of the 'box'. The line cd is
the line of minimum slope and the line ef
is the line of maximum slope.
If the slope of the best straight line has a value of
S and the error in its value is
ΔS, then
Δ S = (max. slope - min. slope) /
(2√n)
Similarly, if the value of the intercept is I,
and the error in its value is ΔI, then
ΔI = (max. intercept - min.
intercept) / (2√n)
n = number of points enclosed in the 'box'.
The fractional error in the slope is given by
ΔS/S, and the percentage error in the
slope is given by (ΔS/S) x 100. If a
parameter P is derived directly from the slope, say, by
multiplication or division then ΔS/S =
ΔP/P, i.e. the fractional error in the slope has
the same value as the fractional error in the parameter P.
Note.
If you are using Microsoft Excel it is
possible to obtain these errors using the LINEST function.
- Enter the X and Y values for which you wish to do the analysis
- Highlight a range for the output of the analysis (This should be
2 columns wide and 4 rows deep and away from your X,Y points)
- enter the formula for LINEST.
For example, =LINEST(b2.b12,a2.a12,TRUE,TRUE)
then hit the Control,Shift,Enter keys simultaneously
- the slope and intercept are in the first row of the output
and the error in the slope and the intercept are in the second
row of the output. The correlation coefficient is in the third
row.
Alternatively, plot the XY data then, after selecting a point, choose
Add Trendline from the Chart menu. The first tab shows Type and for this
you can select Linear, the second tab shows Options and you can select
Display equation on chart and if desired force the intercept through
a specific point, e.g. zero.
The output will show only the slope and intercept and not the errors or
correlation coefficient.
 Return to Chemistry,
UWI-Mona, Home Page
Return to Chemistry,
UWI-Mona, Home Page
Copyright © 2006 by Robert John Lancashire,
all rights reserved.
Created and maintained by Prof. Robert J.
Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.
Created Nov 2002. Links checked and/or last
modified 14th March 2006.
URL
http://wwwchem.uwimona.edu.jm/lab_manuals/c10appendix7.html

 Return to Chemistry,
UWI-Mona, Home Page
Return to Chemistry,
UWI-Mona, Home Page